Tag Archive

You are currently browsing the tag archive for the ‘Quasiconvex subgroups’ tag.

35. Separating quasi-convex subgroups.

22 April 2009 in Course notes | Tags: Quasiconvex subgroups, Separability | by pweil | Leave a comment

Last time: Theorem 21 (Groves–Manning–Osin): If $G$ is hyperbolic rel $\mathcal P$ then there exists a finite subset $A \subseteq G\setminus 1$ such that if $\bigcup_i N_i \cap A = \emptyset$ then
(a) $P_i/N_i \to G/\mathcal N$ is injective;
(b) $G$ is hyperbolic rel $P_i/N_i$ .

Theorem 22 (Gromov, Olshanshkii, Delzant): If $G$ is hyperbolic relative to the infinite cyclic $\{\langle g_1\rangle,\dots,\langle g_n \rangle\}$ then there is a $K>0$ such that for all $l_1,\dots,l_n>0$ there exists a $\phi : G \to G'$ hyperbolic such that $o(\phi(g_i))=Kl_i$ for each $i$ .

The proof is an easy application of Groves–Manning–Osin.

Definition: If $\{\langle g_1 \rangle,\dots,\langle g_n\rangle\}$ (infinite cyclic) is malnormal then we say $g_1,\dots,g_n$ are independent. A group G is omnipotent if for every independent $g_1,\dots,g_n$ there exists a $K>0$ such that for all $l_1,\dots,l_n>0$ there exists a homomorphism $\phi$ from $G$ to a finite group such that $o(\phi(g_i)) = Kl_i$ for all $i$ .

Omnipotence strengthens residual finiteness for torsionfree groups.

Exercise 29: If every hyperbolic group is residually finite then every hyperbolic group is omnipotent.

We’ll finish off by talking about a similar theorem of Agol–Groves–Manning. I’m going to seem a little cavalier about torsion. This is OK. In fact, if every hyperbolic group is residually finite then every hyperbolic group is virtually torsionfree.

Theorem 22 (Agol–Groves–Manning): If every hyperbolic group is residually finite then every quasi-convex subgroup $H$ of any hyperbolic group $G$ is separable.

Let $g \in G \setminus H$ . The idea is to Dehn fill $H$ to get a new hyperbolic group $\bar G$ in which the image $\bar H$ is finite and $\bar g \not\in\bar H$ . If we could do this, we would be done by residual finiteness. This works if $H$ is malnormal. But it probably isn’t. Fortunately, we can quantify how far $H$ is from being malnormal:

Definition: The height of $H$ is the maximal $n \in \mathbb N$ such that there are distinct cosets $g_1 H,\dots,g_n H \in G/H$ such that the intersection
$g_1 H g_1^{-1} \cap \dots \cap g_n H g_n^{-1}$
is infinite.

H is height $0$ iff $H$ is finite. In a torsionfree group, $H$ is height $1$ iff $H$ is malnormal.

Theorem 23 (Gitik, Mitra, Rips, Sageev): A quasiconvex subgroup of a hyperbolic group has finite height.

Agol, Groves and Manning are able to prove:

Theorem 24: Let $G$ be a (torsionfree) residually finite hyperbolic group, and $H$ a quasiconvex subgroup of height $k$ . Let $g \in G\setminus H$ . Then is an epimorphism $\eta: G \to \bar G$ to a hyperbolic group such that
(i) $\eta(H)$ is quasiconvex in $\bar G$ ;
(ii) $\eta(g) \not\in\eta(H)$ ;
(iii) $\eta(H)$ has height $\leq k-1$ .

The idea of the proof of Theorem 24 is to Dehn fill a finite index subgroup of a maximal infinite intersection of conjugates of $H$ . Theorem 22 is an easy consequence.

14. Centralizers (continued)

23 February 2009 in Course notes | Tags: Hyperbolic groups, Quasiconvex subgroups | by smhart | 1 comment

Our goal is to understand the abelian subgroups of a hyperbolic group; e.g., can a hyperbolic group contain $\mathbb{Z}^2$ as a subgroup? We already know that it cannot be a quasiconvex subgroup, but it may be possible for $\mathbb{Z}^2$ to be “twisted” in some manner.

Theorem 10. The intersection of two quasiconvex subgroups is quasiconvex.

Pf. As usual, we work in a $\delta$ -hyperbolic $\text{Cay}_S ( \Gamma )$ . Let $H , K \subset \Gamma$ be quasiconvex subgroups each with the same corresponding constant $\kappa$ . Let $\gamma \in H \cap K$ , and let $g_0 \in [ 1 , \gamma ] \cap \Gamma$ . Our goal is therefore to show that $g_0$ is in a bounded neighborhood of $H \cap K$ . Let $g_D$ be the (or more precisely, a particular) closest element of $H \cap K$ to $g_0$ , and suppose that $d ( g_0 , g_D ) = D$ . Let $h_0 \in H$ be such that $d ( g_0 , h_0 ) \leq \kappa$ and let $k_0 \in K$ be such that $d ( g_0 , k_0 ) \leq \kappa$ ; such elements exist since $H$ and $K$ are quasiconvex. Let $g_t \in [ g_0 , g_D ]$ be such that $d ( g_0 , g_t ) = t$ . We sketch the situation below.

Consider the geodesic triangle with vertices $g_0$ , $h_0$ , and $g_D$ . Because this triangle is $\delta$ -slim, for each $t$ there exists some $h_t \in H$ such that $d ( h_t , g_t ) \leq \delta + \kappa$ .

fig2

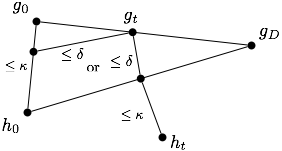
Likewise, for each $t$ there exists $k_t \in K$ such that $d ( g_t , k_t ) \leq \delta + \kappa$ . Next, let $u_t = g_t^{-1} h_t$ and $v_t = g_t^{-1} k_t$ . Then $\ell ( u_t ) , \ell ( v_t ) \leq \delta + \kappa$ .

Suppose $D > ( \# B ( 1 , \delta + \kappa ) )^2$ . Then by the Pigeonhole Principle there are integers $s$ and $t$ with $s > t$ such that $u_s = u_t$ and $v_s = v_t$ . Now, we can use this information to find a closer element of $H \cap K$ .

fig3

Consider $g_t g_s^{-1} g_D$ . By the triangle inequality,

$d ( g_0 , g_t g_s^{-1} g_D ) \leq d ( g_0 , g_t ) + d ( g_t , g_t g_s^{-1} g_D ) = t + D - s < D$ .

All that remains is to prove that $g_t g_s^{-1} g_D \in H \cap K$ . But since $u_t = u_s$ ,

$g_t g_s^{-1} g_D = g_t u_t u_t^{-1} g_s^{-1} g_D = ( g_t u_t ) ( g_s u_s )^{-1} g_D = h_t h_s^{-1} g_D \in H$ .

Playing this same game with $v_t = v_s$ , we get $g_t g_s^{-1} g_D = k_t k_s^{-1} g_D \in K$ , and hence we have found our contradiction. $\square$

For a group $G$ , recall that $Z ( G ) = \{ g \in G : g g' = g' g \text{ for all } g' \in G \}$ is the center of $G$ .

Corollary. For any $\gamma \in \Gamma$ (where $\Gamma$ is $\delta$ -hyperbolic) of infinite order, the subgroup generated by $\gamma$ is quasiconvex. Equivalently, the map $c : \mathbb{Z} \to \text{Cay}_S ( \Gamma )$ sending $n \mapsto \gamma^n$ is a quasigeodesic (which is a sensible statement to make given that $\mathbb{Z}$ is quasi-isometric to $\mathbb{R}$ ).

Pf. By Theorem 9, we deduce that $C ( \gamma )$ is quasiconvex, and so is finitely generated. Let $T$ be a finite generating set for $C ( \gamma )$ . Notice

$Z ( C ( \gamma ) ) = \displaystyle \bigcap_{t\in T} C_{C(\gamma)} ( t )$

where $C_{C(\gamma)} ( t )$ is the centralizer in $C ( \gamma )$ of $t$ , so $Z ( C ( \gamma ) )$ is quasiconvex by Theorem 10 and thus $Z ( C ( \gamma ) )$ is a finitely generated abelian group containing $\langle \gamma \rangle$ . By Exercise 16 (below), we deduce that $\langle \gamma \rangle$ is quasi-isometrically embedded in $Z ( C ( \gamma ) )$ , and hence is quasiconvex in $\Gamma$ . $\square$

Exercise 16. Cyclic subgroups of finitely generated abelian groups are quasi-isometrically embedded.

Lemma 10. Suppose the order of $\gamma \in \Gamma$ is infinite. If $\gamma^p$ is conjugate to $\gamma^q$ , then $| p | = | q |$ .

Pf. Suppose $t \gamma^p t^{-1} = \gamma^q$ . An easy induction on $n$ shows $t^n \gamma^{(p^n)} t^{-n} = \gamma^{(q^n)}$ . Therefore, applying the triangle inequality,

$\ell ( \gamma^{(q^n)} ) \leq \ell ( \gamma^{(p^n)} ) + 2 \ell ( t^n ) \leq | p |^n \ell ( \gamma ) + 2 n \ell ( t )$ .

But $\langle \gamma \rangle \hookrightarrow \Gamma$ is a $( \lambda , \epsilon )$ -quasi-isometric embedding, so

$| p |^n \ell ( \gamma ) + 2 n \ell ( t ) \geq \ell ( \gamma^{(q^n)} ) \geq \lambda^{-1} | q |^n - \epsilon$ .

This is impossible unless $| q | \leq | p |$ (eventually the exponential growth dominates). Similarly, reversing the roles of $p$ and $q$ in the above argument implies that $| p | \leq | q |$ , so $| p | = | q |$ . $\square$

13. Conjugacy & Centralizers

22 February 2009 in Course notes | Tags: Hyperbolic groups, Quasiconvex subgroups | by dgirao | Leave a comment

Theorem 8: Let $\Gamma$ be a $\delta$ -hyperbolic group with respect to $S$ . If $u,v \in \Gamma$ are conjugate then there exists $\gamma\in\Gamma$ such that

$\gamma u\gamma^{-1}=v\\l(\gamma)\leq M(l(u),l(v))$

where $M$ depends only on $\Gamma$ .

Proof: We work in $Cay_S(\Gamma)$ . Let $\gamma\in \Gamma$ be such that $\gamma u\gamma^{-1}=v$ . Let $\gamma_t \in [1,\gamma]$ be such that $d(1,\gamma_t)=t$ . We want to find a bound on $d(\gamma_t, v\gamma_t)$ .

Let $c=[1,\gamma u]$ . By Lemma 9,

$d(\gamma_t,c(t))\leq 2(\delta+l(v))\\ d(v\gamma_t,c(l(\gamma u)-(l(\gamma)-t)))\leq 2(\delta+l(v))$

Also

$d(c(t),c(l(\gamma u)-(l(\gamma)-t)))=l(\gamma u)-l(\gamma)+t-t\\=l(\gamma u)-l(\gamma)\leq l(u)$

So $d(\gamma_t,v\gamma_t)\leq 4(\delta +l(u)+l(v))= R(l(u),l(v))$ . Thus $l(\gamma_t^{-1}v\gamma_t)\leq R$ . Suppose that $l(\gamma)> \#B(1,R)$ . By the Pigeonhole Principle there exist integers $s>t$ such that $\gamma_t^{-1}v\gamma_t=\gamma_s^{-1}v\gamma_s$ . It follows that one can find a shorter conjugating element by cutting out the section of $\gamma$ between $\gamma_t$ and $\gamma_s$ .

Recall, for $\gamma \in \Gamma$ , $C(\gamma)=\{g\in\Gamma: g\gamma=\gamma g\}$ is the centralizer of $\gamma$ .

Theorem 9: If $\Gamma$ is $\delta$ -hyperbolic with respect to $S$ and $\gamma\in\Gamma$ , then $C(\gamma)$ is quasi-convex in $\Gamma$ .

Proof: Again we work in $Cay_S(\Gamma)$ . Let $g\in C(\gamma)$ , $h\in [1,g]$ . We need to prove that $H$ is in a bounded neighborhood $C(\gamma)$ .