392C Geometric Group Theory

35. Separating quasi-convex subgroups.

22 April 2009 in Course notes | Tags: Quasiconvex subgroups, Separability | by pweil | Leave a comment

Last time: Theorem 21 (Groves–Manning–Osin): If $G$ is hyperbolic rel $\mathcal P$ then there exists a finite subset $A \subseteq G\setminus 1$ such that if $\bigcup_i N_i \cap A = \emptyset$ then
(a) $P_i/N_i \to G/\mathcal N$ is injective;
(b) $G$ is hyperbolic rel $P_i/N_i$ .

Theorem 22 (Gromov, Olshanshkii, Delzant): If $G$ is hyperbolic relative to the infinite cyclic $\{\langle g_1\rangle,\dots,\langle g_n \rangle\}$ then there is a $K>0$ such that for all $l_1,\dots,l_n>0$ there exists a $\phi : G \to G'$ hyperbolic such that $o(\phi(g_i))=Kl_i$ for each $i$ .

The proof is an easy application of Groves–Manning–Osin.

Definition: If $\{\langle g_1 \rangle,\dots,\langle g_n\rangle\}$ (infinite cyclic) is malnormal then we say $g_1,\dots,g_n$ are independent. A group G is omnipotent if for every independent $g_1,\dots,g_n$ there exists a $K>0$ such that for all $l_1,\dots,l_n>0$ there exists a homomorphism $\phi$ from $G$ to a finite group such that $o(\phi(g_i)) = Kl_i$ for all $i$ .

Omnipotence strengthens residual finiteness for torsionfree groups.

Exercise 29: If every hyperbolic group is residually finite then every hyperbolic group is omnipotent.

We’ll finish off by talking about a similar theorem of Agol–Groves–Manning. I’m going to seem a little cavalier about torsion. This is OK. In fact, if every hyperbolic group is residually finite then every hyperbolic group is virtually torsionfree.

Theorem 22 (Agol–Groves–Manning): If every hyperbolic group is residually finite then every quasi-convex subgroup $H$ of any hyperbolic group $G$ is separable.

Let $g \in G \setminus H$ . The idea is to Dehn fill $H$ to get a new hyperbolic group $\bar G$ in which the image $\bar H$ is finite and $\bar g \not\in\bar H$ . If we could do this, we would be done by residual finiteness. This works if $H$ is malnormal. But it probably isn’t. Fortunately, we can quantify how far $H$ is from being malnormal:

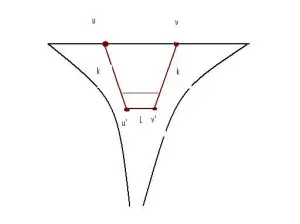
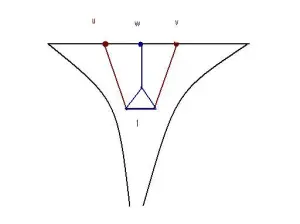
Definition: The height of $H$ is the maximal $n \in \mathbb N$ such that there are distinct cosets $g_1 H,\dots,g_n H \in G/H$ such that the intersection
$g_1 H g_1^{-1} \cap \dots \cap g_n H g_n^{-1}$
is infinite.

H is height $0$ iff $H$ is finite. In a torsionfree group, $H$ is height $1$ iff $H$ is malnormal.

Theorem 23 (Gitik, Mitra, Rips, Sageev): A quasiconvex subgroup of a hyperbolic group has finite height.

Agol, Groves and Manning are able to prove:

Theorem 24: Let $G$ be a (torsionfree) residually finite hyperbolic group, and $H$ a quasiconvex subgroup of height $k$ . Let $g \in G\setminus H$ . Then is an epimorphism $\eta: G \to \bar G$ to a hyperbolic group such that
(i) $\eta(H)$ is quasiconvex in $\bar G$ ;
(ii) $\eta(g) \not\in\eta(H)$ ;
(iii) $\eta(H)$ has height $\leq k-1$ .

The idea of the proof of Theorem 24 is to Dehn fill a finite index subgroup of a maximal infinite intersection of conjugates of $H$ . Theorem 22 is an easy consequence.

34. Combinatorial Dehn Filling

20 April 2009 in Course notes | Tags: Hyperbolic groups, Relatively hyperbolic groups | by jmaciejewski | Leave a comment

Recall, that for any graph $\Gamma$ we built a combinatorial horoball $\mathcal{H}(\Gamma)$ . For a group $G$ and a collection of subgroups $\mathcal{P}=\{P_1,\ldots,P_n\}$ and a generating set $S$ , we built the augmented Cayley graph $X$ by gluing copies of $\mathcal{H}(\mathrm{Cay}(G))$ . $G$ is hyperbolic relative to $\mathcal{P}$ if and only if $X$ is Gromov hyperbolic.

Exercise 28: If $A$ and $B$ are finitely generated, then $A*B$ is hyperbolic relative $\{A,B\}$ . (Hint: $X$ is a graph of spaces with underlying graph a tree and the combinatorial horoballs for vertex spaces.)

Example: Suppose $M$ is a complete hyperbolic manifold of finite volume. So, $\Gamma=\pi_1M$ acts on $\mathbb{H}^n$ . Let $\Lambda$ be a subset of $\partial\mathbb{H}^n$ consisting of points that are the unique fixed point of some element of $\Gamma$ . So $\Gamma$ acts on $\Lambda$ , and there only finitely many orbits. Let $P_1,\ldots,P_n$ be stabilizers of representatives from these orbits and let $\mathcal{P}=\{P_1,\ldots,P_n\}$ . Then, $\Gamma$ is hyperbolic relative to $\mathcal{P}$ .

Example: Let $G$ be a torsion-free word-hyperbolic group. Then, $G$ is clearly hyperbolic relative to $\{1\}$ . A collection of subgroups $P_1,ldots,P_n$ is malnormal if for any $g\in G$ , $P_i\cap gP_jg^{-1}\neq1$ implies that $i=j$ and $g\in P_i$ . $G$ is hyperbolic relative to $\mathcal{P}=\{P_1,\ldots,P_n\}$ if and only if $\mathcal{P}$ is malnormal.

The collection of subgroups $\mathcal{P}$ is the collection of peripheral subgroups.

Lemma 31: If $G$ is torsion-free and hyperbolic relative to a set of quasiconvex subgroups $\mathcal{P}$ , then $\mathcal{P}$ is malnormal.

Sketch of Proof: Suppose that $P_1\cap gP_2g^{-1}$ is infinite. Consider the following rectangles: Note that if $k=l(g)$ , then $gP_2g^{-1}$ is contained in a $k$ -neighborhood of $gP_2$ . Now, there exists infinite sequences $p_i\in P_1$ and $q_i\in P_2$ such that $d(p_i,gq_i)\leq k$ . Look at the rectangles with vertices $1, g, gp_i, p_i$ . The geodesics in $X$ between 1 and $p_i$ and $g$ and $gq_i$ go arbitrarily deep into the combinatorial horoballs. Therefore, they are arbitrarily far apart. It follows that these rectangles cannot be uniformly slim.

Let $\mathcal{N}=\{N_1,\ldots,N_n\}$ where each $N_i\lhd P_i$ . Write $G/\langle\langle\bigcup_iN_i\rangle\rangle=G/\mathcal{N}$ . Call this the Dehn filling of $G$ .

Note: If $G$ is hyperbolic relative to $\mathcal{P}$ , then $G$ is hyperbolic.

Theorem 21: (Groves-Manning-Osin). Suppose $G$ is hyperbolic relative to $\mathcal{P}$ . Then, there exists a finite set $A$ contained in $G\smallsetminus 1$ such that whenever $(\bigcup_i N_i)\cap A\neq\emptyset$ we have

$P_i/N_i\to G/\mathcal{N}$ is injective for all $i$ , and
$G/\mathcal{N}$ is hyperbolic relative to the collection $\{P_i/N_i\}$ ;

In particular, if $P_i/N_i$ are all hyperbolic, then so is $G/\mathcal{N}$ .

One application of this theorem is a simple proof of a theorem of Gromov, Olshanskii, and Delzant:

Theorem 22: Let $G$ be hyperbolic and suppose $\{\langle g_1\rangle,\ldots,\langle g_n\rangle\}$ is malnormal, with each $\langle g_i\rangle$ infinite. Then, there is constant $K$ such that for all positive integers $l_1,\ldots,l_n$ there is an epimorphism to a hyperbolic group $\phi:G\to G'$ such that $o(\phi(g_i))=Kl_i$ for each $i$ .

33. Relatively Hyperbolic Groups

19 April 2009 in Course notes | Tags: Relatively hyperbolic groups | by elandes | 1 comment

Some intuition: Recall that if $M$ is a closed hyperbolic manifold
then $\pi_1(M)$ is word-hyperbolic. However, a lot of interesting hyperbolic manifolds are not closed.

Example: Let $K\subset S^3$ be the figure 8 knot.

Then the complement $M_{8}=S^{3}$ $K$ admits a complete hyperbolic metric and is of finite volume.

So, here we have an example of a hyperbolic manifold which is not compact but is of finite volume. This is almost as which is almost as natural as being closed.

$M_{8}$ is homotopy equivalent to $M_{8}'$ , the complement of a thickened $K$ in $S^{3}$ .

fig2

$M_8'$ is a compact manifold with boundary and its interior admits a hyperbolic metric. The boundary of $M_8'$ is homeomorphic to a 2-torus, so $\partial M_8' \hookrightarrow M_8'$ induces a map $\mathbb{Z}^2\hookrightarrow\pi_1M_8'$ . By Dehn’s lemma, the map is injective so $\pi_1M_8'$ cannot be word hyperbolic. The point is that $\pi_1M_8$ acts nicely on $\mathbb{H}^2$ but no cocompactly so the Svarc=Milnor lemma does not apply.

The torus boundary component of $M_8'$ corresponds to a cusp of $M_8$ .

The point is that we can use cusped manifolds like $M_8'$ to build a lot of manifolds and in particular a lot of hyperbolic manifolds.

Take $M_8'$ and a solid Torus $T$ .

Choose a homeomorphism $\phi: \partial M_8' \hookrightarrow\partial T$

Definition: The manifold $M_{\phi}=M_{8}'\cup_{\phi}T$ is obtained from $M_{8}'$ by Dehn filling .

We now want to understand what we have done to $\pi_{1}M_{8}$ . The map $\phi$ induces a map $\phi_{*}$ :

lecture_4_17_09_xymatrix1

The surjectivity of $\phi_{*}$ follows from the fact that $\phi$ is a homeomorphism. The Seifert Van Kampen theorem implies that $\pi_{1}M_{\phi}=\pi_{1}M_{8}\langle\langle \ker(\phi_{*})\rangle\rangle$ , where $\langle\langle\ker(\phi_{*}) \rangle\rangle$ denotes the normal closure of $\ker(\phi_{*})$ .

Gromov-Thurston $2\pi$ theorem: Let M be any compact hyperbolic manifold and $\partial_{0}M$ be a component of $\partial M$ homeomorphic to a 2-torus for all but finitely many choices of

lecture_4_17_09_xymatrix2

the Dehn filling $M_{\phi}$ is hyperbolic.

Note: by finitely many we mean finitely many maps up to homotopy.

This is a very fruitful way of building hyperbolic manifolds. The next question to ask is whether we can do the same thing for groups. So, now we will try to develop a group theoretic version of this picture.

Let $\Gamma$ be a group theoretic graph with the induced length metric. Construct a new graph $\mathcal{H}(\Gamma)$ called the combinatorial horoball on $\Gamma$ as follows: Define the vertices $V(\mathcal{H})=V(\Gamma)\times \mathbb{N}$ . There are two sorts of edges in ${E}(\mathcal{H})$ . We say that $(u,k)$ and $(v,k)$ are joined by a (horizontal) edge if $d_{\Gamma}(u,v) \leq 2^{k}$ and $u\neq v$ . We say that $(v,k)$ and $(v,k+1)$ are joined by a (vertical) edge for all $k$ .

fig6
For $k$ large enough $u'$ and $v'$ will have distance one and $L\leq 1$ iff $2^{k} \ge d_{\Gamma}(u,v)$ iff $k\leq \log_{2}d_{\Gamma}(u,v)$ .

Exercise 27:
(A). For $u,vin V(\Gamma)$ , $d_{\mathcal{H}}((u,0),(v,0))\approx \log_{2}d_{\Gamma}(u,v)$ .

(B). For any connected $\Gamma$ , $\mathcal{H}(\Gamma)$ is Gromov hyperbolic .

fig7

Let $G$ be a group and let $\mathcal{P}=\{ P_{1},\ldots, P_{n} \}$ be a finite set of finitely generated subgroups of $G$ . Choose a finite generating set $S$ for $G$ such that for each $i$ , $s_i=S \cap P_i$ generate $P_i$ . Then $\mathrm{Cay}(G,S)$ contains natural copies of $\mathrm{Cay}(P_{i},S_{i})$ .

Construct the augmented Cayley graph $X=X(G,\mathcal{P},S)$ by gluing on combinatorial horoballs equivariantly.

$X(G,\mathcal{P},S) = \mathrm{Cay}(G,S) \cup \bigcup_{i} \lbrack \mathcal{H}(\mathrm{Cay}(P_{i},S_{i})) \times G/P_{i} \rbrack / \sim$ where for each $i$
and each $gP_{i}\in G$ / $P_{i}$ , $\mathcal{H}(\mathrm{Cay}(P_{i},S_{i}) \times \{ gP_{i}\}$ is glued to $g\mathrm{Cay}(P_{i},S_{i})$ along $\mathrm{Cay}(P_{i},S_ {i}) \times \{ 0 \}$ .