You are currently browsing elandes’s articles.
Some intuition: Recall that if is a closed hyperbolic manifold
then is word-hyperbolic. However, a lot of interesting hyperbolic manifolds are not closed.
Example: Let be the figure 8 knot.
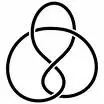
Then the complement
admits a complete hyperbolic metric and is of finite volume.
So, here we have an example of a hyperbolic manifold which is not compact but is of finite volume. This is almost as which is almost as natural as being closed.
is homotopy equivalent to
, the complement of a thickened
in
.

is a compact manifold with boundary and its interior admits a hyperbolic metric. The boundary of
is homeomorphic to a 2-torus, so
induces a map
. By Dehn’s lemma, the map is injective so
cannot be word hyperbolic. The point is that
acts nicely on
but no cocompactly so the Svarc=Milnor lemma does not apply.
The torus boundary component of corresponds to a cusp of
.

The point is that we can use cusped manifolds like to build a lot of manifolds and in particular a lot of hyperbolic manifolds.
Take and a solid Torus
.
Choose a homeomorphism
Definition: The manifold is obtained from
by Dehn filling .
We now want to understand what we have done to . The map
induces a map
:
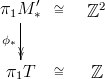
The surjectivity of follows from the fact that
is a homeomorphism. The Seifert Van Kampen theorem implies that
, where
denotes the normal closure of
.
Gromov-Thurston theorem: Let M be any compact hyperbolic manifold and
be a component of
homeomorphic to a 2-torus for all but finitely many choices of
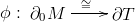
the Dehn filling is hyperbolic.
Note: by finitely many we mean finitely many maps up to homotopy.
This is a very fruitful way of building hyperbolic manifolds. The next question to ask is whether we can do the same thing for groups. So, now we will try to develop a group theoretic version of this picture.
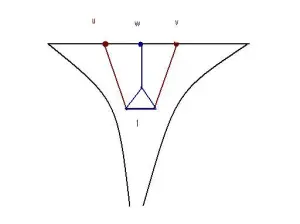
Let be a group theoretic graph with the induced length metric. Construct a new graph
called the combinatorial horoball on
as follows: Define the vertices
. There are two sorts of edges in
. We say that
and
are joined by a (horizontal) edge if
and
. We say that
and
are joined by a (vertical) edge for all
.
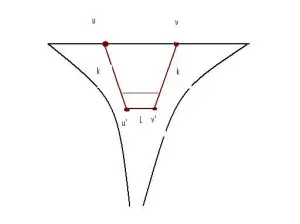
For large enough
and
will have distance one and
iff
iff
.
Exercise 27:
(A). For ,
.
(B). For any connected ,
is Gromov hyperbolic .
Let be a group and let
be a finite set of finitely generated subgroups of
. Choose a finite generating set
for
such that for each
,
generate
. Then
contains natural copies of
.
Construct the augmented Cayley graph by gluing on combinatorial horoballs equivariantly.
where for each
and each /
,
is glued to
along
.
Definition: G is hyperbolic rel if and only if
is Gromov hyperbolic for some (any) choice of
.
Theorem 12 (Gromov): Let be torsion-free
-hyperbolic group. If
such that
, then for all sufficiently large
,
.
Remark: The torsion-free hypothesis is not necessary, but it allows us to avoid some technicalities. For instance, it is a non-obvious fact that an infinite hyperbolic group contains a copy of .
For the rest of this lecture will be a torsion-free
-hyperbolic group,
where
are primitive (i.e. not proper powers).
Recall that for torsion-free
-hyperbolic,
primitive implies that
.
If and
do not commute we can show there is some point
on
arbitrarily far from
.
 Hence we have the following lemma.
Hence we have the following lemma.
Lemma 13:
If and
do not commute there is some point
on
arbitrarily far from
.
Proof: Suppose not. That means such that
such that
. So
is in
. But the Cayley graph is locally finite so
has finitely many elements. By the Pigeonhole Principle
such that
for some
. Then
. But then
.
.
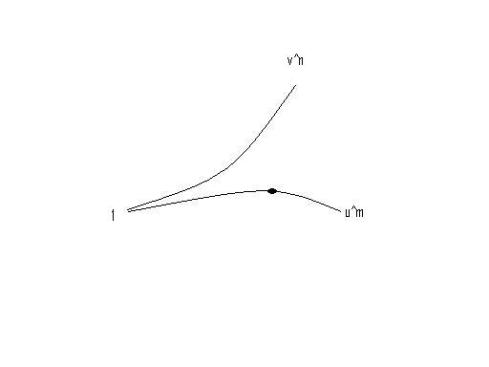
For a moment view and
as the horizontal and vertical geodesics in
. For two points
on
and
on
, we can argue that the geodesic between them curves toward the origin.
 And so we have Lemma 14.
And so we have Lemma 14.
Lemma 14: There exists such that
,
.
Proof:
 Recall that
Recall that by
is a quasi-isometric embedding. So by Theorem 6,
and
 By Lemma 13 choose
By Lemma 13 choose such that
. Choose
such that
. Now,
must be
-close to
so for some point
on the geodesic between
and
,
. Then
.
For a subgroup , one can choose a closest point projection
which is
-equivariant. (Write
. Choose
where
and
are close and declare
to be
-equivariant.)
is typically not a group homomorphism.
We’re interested in and
.
 In
In , there is some
such that
either
or
.

Lemma 15: such that
,
or
.
Proof:
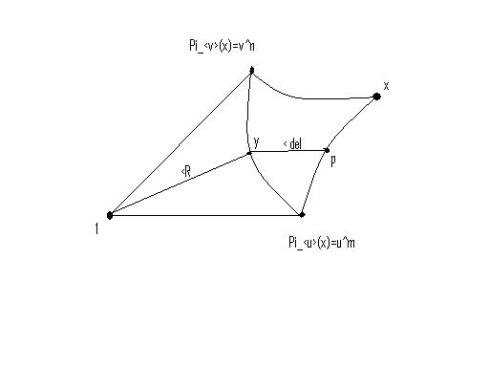
Let . WLOG,
is
-close to
and
since
is the closest point to
(in particular compared to
). So
.
.
Now we can prove the theorem.
Proof of Theorem 12:
The idea is to use the Ping-Pong Lemma on the Cayley graph.
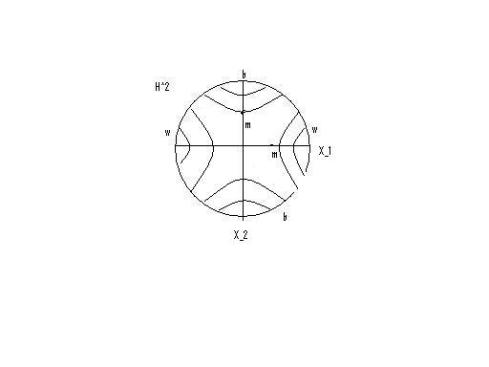 Let
Let and let
, where
is provided by Lemma 15. For all
we have
and likewise for all
we have
. In particular,
.
Let . By
-equivariance,
for any . In particular,
by the triangle inequality. Similarly,
for all and all
. Because
and
are quasi-isometrically embedded, it follows that
and
for
.
Therefore, by the Ping-Pong Lemma .
Recent Comments