You are currently browsing the tag archive for the ‘Hyperbolic groups’ tag.
Recall, that for any graph we built a combinatorial horoball
. For a group
and a collection of subgroups
and a generating set
, we built the augmented Cayley graph
by gluing copies of
.
is hyperbolic relative to
if and only if
is Gromov hyperbolic.
Exercise 28: If and
are finitely generated, then
is hyperbolic relative
. (Hint:
is a graph of spaces with underlying graph a tree and the combinatorial horoballs for vertex spaces.)
Example: Suppose is a complete hyperbolic manifold of finite volume. So,
acts on
. Let
be a subset of
consisting of points that are the unique fixed point of some element of
. So
acts on
, and there only finitely many orbits. Let
be stabilizers of representatives from these orbits and let
. Then,
is hyperbolic relative to
.
Example: Let be a torsion-free word-hyperbolic group. Then,
is clearly hyperbolic relative to
. A collection of subgroups
is malnormal if for any
,
implies that
and
.
is hyperbolic relative to
if and only if
is malnormal.
The collection of subgroups is the collection of peripheral subgroups.
Lemma 31: If is torsion-free and hyperbolic relative to a set of quasiconvex subgroups
, then
is malnormal.
Sketch of Proof: Suppose that is infinite. Consider the following rectangles: Note that if
, then
is contained in a
-neighborhood of
. Now, there exists infinite sequences
and
such that
. Look at the rectangles with vertices
. The geodesics in
between 1 and
and
and
go arbitrarily deep into the combinatorial horoballs. Therefore, they are arbitrarily far apart. It follows that these rectangles cannot be uniformly slim.
Let where each
. Write
. Call this the Dehn filling of
.
Note: If is hyperbolic relative to
, then
is hyperbolic.
Theorem 21: (Groves-Manning-Osin). Suppose is hyperbolic relative to
. Then, there exists a finite set
contained in
such that whenever
we have
is injective for all
, and
is hyperbolic relative to the collection
;
In particular, if are all hyperbolic, then so is
.
One application of this theorem is a simple proof of a theorem of Gromov, Olshanskii, and Delzant:
Theorem 22: Let be hyperbolic and suppose
is malnormal, with each
infinite. Then, there is constant
such that for all positive integers
there is an epimorphism to a hyperbolic group
such that
for each
.
Theorem 12 (Gromov): Let be torsion-free
-hyperbolic group. If
such that
, then for all sufficiently large
,
.
Remark: The torsion-free hypothesis is not necessary, but it allows us to avoid some technicalities. For instance, it is a non-obvious fact that an infinite hyperbolic group contains a copy of .
For the rest of this lecture will be a torsion-free
-hyperbolic group,
where
are primitive (i.e. not proper powers).
Recall that for torsion-free
-hyperbolic,
primitive implies that
.
If and
do not commute we can show there is some point
on
arbitrarily far from
.
 Hence we have the following lemma.
Hence we have the following lemma.
Lemma 13:
If and
do not commute there is some point
on
arbitrarily far from
.
Proof: Suppose not. That means such that
such that
. So
is in
. But the Cayley graph is locally finite so
has finitely many elements. By the Pigeonhole Principle
such that
for some
. Then
. But then
.
.
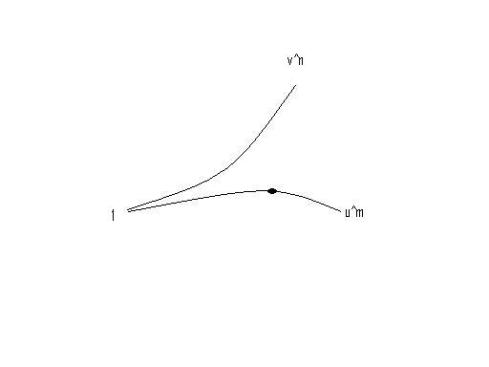
For a moment view and
as the horizontal and vertical geodesics in
. For two points
on
and
on
, we can argue that the geodesic between them curves toward the origin.
 And so we have Lemma 14.
And so we have Lemma 14.
Lemma 14: There exists such that
,
.
Proof:
 Recall that
Recall that by
is a quasi-isometric embedding. So by Theorem 6,
and
 By Lemma 13 choose
By Lemma 13 choose such that
. Choose
such that
. Now,
must be
-close to
so for some point
on the geodesic between
and
,
. Then
.
For a subgroup , one can choose a closest point projection
which is
-equivariant. (Write
. Choose
where
and
are close and declare
to be
-equivariant.)
is typically not a group homomorphism.
We’re interested in and
.
 In
In , there is some
such that
either
or
.

Lemma 15: such that
,
or
.
Proof:
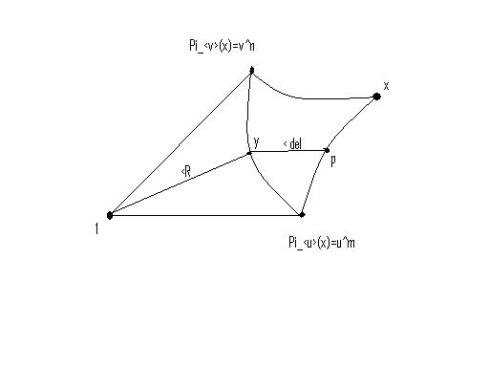
Let . WLOG,
is
-close to
and
since
is the closest point to
(in particular compared to
). So
.
.
Now we can prove the theorem.
Proof of Theorem 12:
The idea is to use the Ping-Pong Lemma on the Cayley graph.
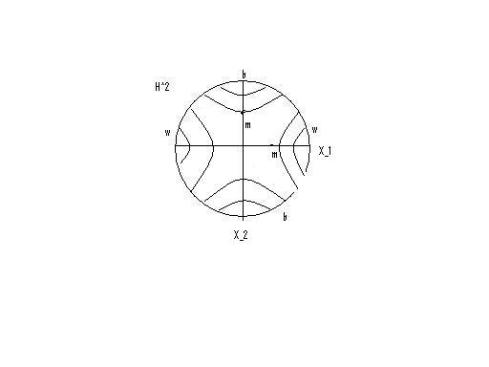 Let
Let and let
, where
is provided by Lemma 15. For all
we have
and likewise for all
we have
. In particular,
.
Let . By
-equivariance,
for any . In particular,
by the triangle inequality. Similarly,
for all and all
. Because
and
are quasi-isometrically embedded, it follows that
and
for
.
Therefore, by the Ping-Pong Lemma .
Finally, we are in a position to prove that a hyperbolic group has no subgroup isomorphic to .
Theorem 11. Let with
. Then
.
Proof. By Lemma 10, we can assume that is not conjugate to any element of length
by replacing
with a power of itself. Suppose
. We need to bound
.

Replacing with
for some
, we may assume that
. We will be done if we can bound
.
Suppose . By dividing into triangles, we see that any geodesic rectangle is
-slim, in the same way that triangles are
-slim.
Because the rectangle with vertices is
-slim, there exists
such that
.
If , then
, a contradiction. Similarly
. So
. Therefore,
.
But . This is a contradiction since we assumed that
is not conjugate to anything so short. Therefore
. Thus
.
An element of a group is torsion if its order is finite.
A group is torsion if every element is torsion.
A group is torsion-free if no nontrivial elements are torsion.
Corollary. Every non-trivial abelian subgroup of a hyperbolic group is virtually cyclic.
Lemma 11. Let be a torsion-free hyperbolic group. Whenever
is not a proper power, then
is malnormal.
Definition. A subgroup of a group
is malnormal if for all
,
, then
.
Remark. By Theorem 11, if is hyperbolic and torsion-free, centralizers are cyclic.
Proof of Lemma. Suppose .
Therefore for some ,
.
By Lemma 10, . Therefore
. Thus
. Therefore
.
Exercise 17. Prove that if where
is hyperbolic and torsion-free and
and
and
, then
. That is,
is commutative transitive.
We now turn briefly to a fundamental open question about hyperbolic groups. This question is a theme of the course.
Question. Is every word-hyperbolic group residually finite?
The fundamental groups of hyperbolic manifolds are linear, so residually finite by Selberg’s Lemma.
What about for negative curved manifolds?
Evidence for:
Theorem (Sela). Every torsion-free hyperbolic group is Hopfian.
Theorem (I. Kapovich-Wise). If every nontrivial hyperbolic group has a proper finite-index subgroup, then every hyperbolic group is residually finite.
Evidence against:
Theorem (Agol-Groves-Manning). If every hyperbolic group is residually finite, then every quasi-convex subgroup of every hyperbolic group is separable.
Recent Comments