Monthly Archive

You are currently browsing the monthly archive for March 2009.

24. Induced graphs of groups and spaces

27 March 2009 in Course notes | Tags: Bass-Serre Theory, Elevations, Graphs of groups | by opsiser | Leave a comment

Our goal is to understand the structure of subgroups of graphs of groups. This will enable us to prove things like: $F \ast_{z} F$ is LERF.

Exercise 22. A group is coherent if every fg subgroup is fp. Prove that $\pi_1$ of a finite graph of groups with coherent vertex groups and cyclic edge group is coherent.

Recall, that if $H \subseteq \pi_1 \mathcal{G}=G$ is fg then H has an induced graph of groups structure. $\mathcal{H} =H \backslash T_H \subseteq H \backslash T$ where T is the Bass-Serre tree of $\mathcal{G}$ .

Topologically, $H$ defines a covering space $X^H \rightarrow X_g$ , which inherits a graph of spaces structure with underlying graph $H\backslash T$ .

$\Gamma' =H \backslash T_H \subseteq H \backslash T$ is a finite connected subgraph and the image of $\Gamma'$ in $X^H$ is a connected subcomplex $X'$ such that $\pi_1 X' = \pi_1 X^H =H$ . $X'$ has the structure of a graph of space with underlying graph $\Gamma'$

There is an explicit algebraic description of $H\backslash T$ , which follows immediately from Lemmas 16,17,18.

Lemma 23. (a) The vertices of $H\backslash T$ are in bijection with $\coprod_{v \in V(\Gamma)} H \backslash G/G_v=\coprod_{v \in V(\Gamma)}\{HgG_v\mid g \in G\}$ .

The vertex $HgG_v$ is labelled by: $H \cap gG_vg^{-1}$ , well-defined up to conjugation in $H$ .

(b) The edges of $H\backslash T$ are in bijection with $\coprod_{e \in E(\Gamma)} H \backslash G/G_e$ . The vertex $HgG_e$ is labelled with $H \cap g G_e g ^{-1}$ .

(c) The edges of $H\backslash T$ adjoining the vertex corresponding to $HgG_v$ are in bijection with $\coprod_{e~\mathrm{adjoining}~v} (g^{-1} H g \cap G_v ) \backslash G_v/G_e$ .

Now we will try to understand this topologically. In particular, we will understand the edge maps of a covering space of a graph of spaces.

Let $f:X \rightarrow Y$ be a continuous map and $Y' \rightarrow Y$ a covering map. If $f':X \rightarrow Y'$ makes the diagram commutes, then $f'$ is a lift of $f$ .

Lemma 24. Fix basepoint $x \in X$ , $y=f(x) \in Y$ , and $y' \in Y'$ mapping to $y$ . There is a lift $f':X \rightarrow Y'$ with $f'(x)=y'$ if and only if $f_{\ast} \pi_1(X,x) \subseteq \pi_1(Y',y')$ . Furthermore, if this lift exists it is unique.

It may be impossible to lift at $y'$ . But it is possible if we pass to a covering space. Eg., if $\tilde{X} \rightarrow X$ is the universal cover. Intuitively, an elevation is a minimal lift.

Definition: Let $X,Y,Y', x,y,y'$ be as above. A based connected covering space $(X',x') \rightarrow (X,x)$ together with a based map $f':(X',x')\to (Y',y')$ such that

elevation1

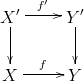
commutes is an elevation (of $f$ at $y'$ ) if whenever the diagram

elevation

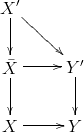
commutes and $X' \rightarrow \bar{X}$ is a covering map of degree larger than 1 then the composition $(\bar{X},\bar{x}) \rightarrow (X,x) \rightarrow (Y,y)$ does not lift to $Y'$ at $y'$ .

The unbased covering map $X' \rightarrow X$ or equivalently the conjugacy class of the subgroup $\pi_1(X') \subseteq \pi_1(X)$ is called the degree of the elevation $f'$ .

23. Isometries of trees, cont.

26 March 2009 in Course notes | Tags: Isometries of trees | by katerman | Leave a comment

Recall from last time:

Theorem 16: Every $\gamma \in \mathrm{Isom}\ T$ is semisimple. If $\gamma$ is loxodromic, then $\mathrm{Min}(\gamma)$ is isometric to $\mathbb{R}$ and $\gamma$ acts on $\mathrm{Min}(\gamma)$ as translation by $|\gamma|$ .

In particular, for every $\langle \gamma \rangle$ , $\mathrm{Min}(\langle \gamma \rangle)$ is a $\langle \gamma \rangle$ -invariant subtree of $T$ .

Exercise 21: If $\gamma, \delta \in \mathrm{Isom}\ T$ and $\mathrm{Min}(\gamma) \cap \mathrm{Min}(\delta) = \emptyset$ , then $\gamma \delta$ is loxodromic, $\mathrm{Min}(\gamma \delta) \cap \mathrm{Min}(\gamma) \neq \emptyset$ , and $\mathrm{Min}(\gamma \delta) \cap \mathrm{Min}(\delta) \neq \emptyset$ .

(Hint: It is enough to construct an axis for $\gamma \delta$ .)

Lemma 20 (Helly’s Theorem for Trees): If $S_1, \ldots, S_n \subseteq T$ are closed subtrees and $S_i \cap S_j \neq \emptyset$ for every $i,j$ , then $\bigcap _i S_i \neq \emptyset$ .

Proof. Case $n=3$ : Let $x_i \in S_j \cap S_k$ where $\{ i,j,k \} = \{1, 2, 3\}$ . Let $o$ be the center of the triangle with vertices $x_1, x_2, x_3$ . Then $o \in S_1 \cap S_2 \cap S_3$ .

General case: Let $S_i ' = S_i \cap S_n$ for $1\leq i \leq n-1$ . Then $S_i' \cap S_j' = S_i \cap S_j \cap S_n \neq \emptyset$ by the $n=3$ case. Now, by induction,

$\bigcap _{i=1} ^n S_i = \bigcap _{i=1}^{n-1} S_i ' \neq \emptyset .$

Corollary: If a finitely generated group $G$ acts on a tree $T$ with no global fixed point, then there is a (unique) $G$ -invariant subtree $T_G$ that is minimal with respect to inclusion, among all $G$ -invariant subtrees. Furthermore, $T_G$ is countable.

Proof. Let

For any $\gamma$ -invariant $T' \subseteq T$ , it is clear that $\mathrm{Axis}(\gamma) \subseteq T'$ . Therefore $T_G$ is minimal. Let $S$ be a finite generating set for $G$ . Suppose that every element of $G$ is elliptical, so for all $s, s' \in S$ , $ss'$ is elliptical. Then for all $s,s' \in S$ ,

$\mathrm{Fix}(s) \cap \mathrm{Fix}(s') \neq \emptyset.$

Therefore by Lemma 20, $\bigcap _{s\in S} \mathrm{Fix}(s) \neq \emptyset,$ a contradiction.

Suppose that $\gamma, \delta \in G$ are loxodromic and $\mathrm{Axis}(\gamma) \cap \mathrm{Axis}(\delta) = \emptyset$ . By Exercise 21, $\mathrm{Axis}(\gamma \delta)$ intersects $\mathrm{Axis}(\gamma)$ and $\mathrm{Axis}(\delta)$ non-trivially. Thus, $T_G$ is connected.

It remains to show that $T_G$ is $G$ -invariant. Let $\gamma, \delta \in G$ . For any $x\in T$ ,

$d(x, \delta ^{-1} \gamma \delta x) = d(\delta x, \gamma(\delta x)).$

This implies that $|\delta^{-1} \gamma \delta | = |\gamma |$ , and

$\delta \mathrm{Axis}(\gamma) = \mathrm{Axis} (\delta^{-1} \gamma \delta).$

So we conclude that $T_G$ is $G$ -invariant.

Definition: If $\Gamma' \subseteq \Gamma$ is connected, then the graph of groups carried by $\Gamma'$ is the graph of groups $\mathcal{G}'$ with underlying graph $\Gamma'$ such that the vertex $v \in V(\Gamma') \subseteq V(\Gamma)$ is labelled by $G_v$ , and the edge $e \in E(\Gamma') \subset E(\Gamma)$ is labelled $G_e$ (with obvious edge maps). There is a natural map $G' \rightarrow G$ , where $G = \pi_1 (\mathcal{G})$ and $G' = \pi_1(\mathcal{G}')$ . This map is an injection by the Normal Form Theorem.

Lemma 21: If $\Gamma$ is countable and $G = \pi_1 \mathcal{G}$ is finitely generated, then there is a finite subgraph $\Gamma' \subset \Gamma$ such that $\pi_1 \mathcal{G}' = \pi_1 \mathcal{G}$ (where $\mathcal{G}'$ is the graph of groups carried by $\Gamma'$ ).

Proof. Let $\Gamma_0 \subseteq \Gamma_1 \subseteq \cdots \subseteq \Gamma$ be an exhaustion of $\Gamma$ by finite connected subgraphs. Let $\mathcal{G}_n$ denote the graph of groups carried by $\Gamma_n$ and set $G_n = \pi_1 (\mathcal{G}_n)$ . Since $G$ is finitely generated, there is an $n$ such that $G_n$ contains each generator of $G$ , and since $G_n \leq G$ , we conclude that $G_n = G$ .

Lemma 22: If $\Gamma$ is countable and $G = \pi_1 \mathcal{G}$ is finitely generated then there is a finite minimal (wrt inclusion) subgraph $\Gamma'$ that carries $G$ .

Proof. Let $T$ be the Bass-Serre tree of $\mathcal{G}$ . Let $\Gamma' = G \backslash T_G \subseteq G \backslash T = \Gamma$ . It’s an easy exercise to check that this is as required.

We will refer to $\Gamma'$ (and $\mathcal{G}'$ , the graph of groups carried by $\Gamma'$ ) as the core of $\mathcal{G}$ .

Theorem 17: If $H \leq G = \pi_1 \mathcal{G}$ is finitely generated, then $H$ decomposes as $\pi_1$ of a finite graph of groups $\mathcal{H}$ . The vertex groups of $\mathcal{H}$ are conjugate into the vertex groups of $\mathcal{G}$ . The edge groups are likewise.

Proof. Let $T$ be the Bass-Serre tree of $\mathcal{G}$ , and set $\mathcal{H} = H \backslash T_H$ .

22. Applications and Isometries of Trees

26 March 2009 in Course notes | Tags: Bass-Serre Theory, Graphs of groups, Isometries of trees | by jhjones998 | Leave a comment

In this lecture, we will use the Normal Form Theorem to understand and construct groups. In particular, we will construct a group that is not residually finite (RF). Note that in the case when $\mathcal{G}$ is an HNN-extension, then the Normal Formal Theorem is called Britton’s Lemma.

Example: The (p,q)-Baumslag-Solitar group has the following presentation:

BSpqgrp

For example $\mathrm{BS} (1,1) \cong \mathbb{Z}^{2}$ .

Consider $\mathrm{BS}(2,3)$ . We will show that this group is non-Hopfian (i.e., that there exists a homomorphism $\varphi: \mathrm{BS}(2,3) \to \mathrm{BS}(2,3)$ that is a surjection with nontrivial kernel), hence is not RF. Consider $\psi: \mathrm{BS}(2,3) \to \mathrm{BS}(2,3)$ defined by $\psi(t) = t$ and $\psi(a) = a^{2}$ . First, we show this is a homomorphism, then a surjection, then that it has nontrivial kernel.

Homomorphism: $\psi(ta^{2}t^{-1}) = ta^{4}t^{-1} = ta^{2}t^{-1}ta^{2}t^{-1} = a^{3}a^{3} = a^{6} = \psi(a^{3}).$ Hence, the map is a homomorphism.

Epimorphism: To see that $\psi$ is a surjection, we check that $a, t \in \mathrm{Im}(\psi)$ . This is obvious for $t$ . Further $a^{2} = \psi(a) \in \mathrm{Im}(\psi)$ and so $ta^{2}t^{-1} = a^{3} \in \mathrm{Im}(\psi)$ . But then $a = a^{3}a^{-2} \in \mathrm{Im}(\psi)$ .

Nontrivial kernel: Consider $c = ata^{-1}t^{-1}a^{-2}tat^{-1}a$ . Then $\psi(c) = a^{2}ta^{-2}t^{-1}a^{-4}ta^{2}t^{-1}a^{2} = a^{2}a^{-3}a^{-4}a^{3}a^{2} = 1$ . So we just need to show that $c$ is nontrivial. We use Britton’s Lemma (Normal Form Theorem). What Britton’s Lemma says is that there will be $t's$ that can be removed from our word using the relation if it is trivial. But this can’t be done with $c$ , so we must have $c \neq 1$ as required.

Remark: $\mathrm{BS}(2,3)$ can never embed in a word-hyperbolic group by a previous Lemma.

Exercise 20: Show that $\mathrm{BS}(1,2) \cong \mathbb{Q}_{2} \rtimes_{2} \mathbb{Z}$ , where $\mathbb{Q}_{2}$ is the dyadic rationals and we have $\mathbb{Z}$ acting via multiplication by 2. One can deduce that $\mathrm{BS}(1,2)$ is linear, hence RF by Selberg’s Lemma.

Theorem 15 (Higman-Neumann-Neumann): Every countable group embeds in a 3-generator group.

Proof: Let $G = \{ 1 = g_{0}, g_{1}, \ldots\}$ . Consider $G \ast \mathbb{Z} = G \ast \langle s \rangle$ . This has some nice free subgroups, unlike $G$ : Let $s_{n} = g_{n}s^{n}$ . Let $\Sigma_{1} = \{ s_{n} \vert n \geq 1\}$ . By the Normal Form Theorem, $\langle \Sigma_{1} \rangle \cong F_{\Sigma_{1}}$ (basically since there will always be some g’s between the s’s whenever you multiply any two elements together). Let $\Sigma_{2} = \{ s_{n} \vert n \geq 2\}$ . Again, $\langle \Sigma_{2} \rangle \cong F_{\Sigma_{2}}$ . Since $latex\Sigma_{1}$ and $\Sigma_{2}$ are both countable, $F_{\Sigma_{1}} \cong F_{\Sigma_{2}}$ .

Consider the HNN-extension $\Gamma = (G \ast \langle s \rangle)\ast_{F_{\Sigma_{1}} \tilde F_{\Sigma_{2}}}$ and let t be the stable letter. For every $n \geq 1$ , $ts_{n}t^{-1} = s_{n+1}$ . But $\Gamma$ is generated by $g_{1}$ , $s$ , and $t$ : $s_{n+1} = ts_{n}t^{-1}$ , so $g_{n+1}s^{n+1} = tg_{n}s^{n}t^{-1}$ or $g_{n+1} = tg_{n}s^{n}t^{-1}s^{-n-1}$ . So by induction $g_{n} \in \langle g_{1}, s, t \rangle$ . for all n. But by construction $\Gamma$ is generated by $\Sigma_{1} \cup \{ s\} \cup \{ t \}$ . $\square$

Remark: In fact 3 can be replaced by 2.

Isometries of Trees

Before we saw that graphs of groups correspond to groups acting on trees. As such, we now turn to isometries of trees. Let $T$ be a tree and let $\gamma \in \mathrm{Isom}(T)$ . The translation length of $\gamma$ is defined to be $|\gamma| := \inf_{x \in T} d(x, \gamma x)$ . Let $\mathrm{Min}(\gamma) = \{ x \in T \vert d(x, \gamma x) = |\gamma| \}$ .

Definition: If $\mathrm{Min}(\gamma) \neq \emptyset$ , $\gamma$ is called semisimple. If $\gamma$ is semisimple, and $|\gamma| = 0$ , $\gamma$ is called elliptic. If $|\gamma| > 0$ , it is called loxodromic.

Theorem 16: Every $\gamma \in \mathrm{Isom}(T)$ is semisimple. If $\gamma$ is loxodromic, $\mathrm{Min}(\gamma)$ is isometric to $\mathbb{R}$ , and $\gamma$ acts on $\mathrm{Min}(\gamma)$ as translation by $|\gamma|$ .

Notation: If $\gamma$ is elliptic, we write $\mathrm{Min}(\gamma) = \mathrm{Fix}(\gamma)$ . If $\gamma$ is loxodromic$, we write $\mathrm{Min}(\gamma) = \mathrm{Axis}(\gamma)$ . Note that $\mathrm{Fix}(\gamma)$ is connected since if we have two points fixed by $\gamma$ any path between them must be fixed, for otherwise we would not be in a tree.

Case 1 of Theorem 16

Proof of Theorem 16: Consider any $x \in T$ and the triangle with vertices $x, \gamma x, \gamma^{2} x$ (i.e., $[x, \gamma x] \cup \gamma [x, \gamma x]$ ). Let $[ x, \gamma x] \cap [ \gamma x, \gamma^{2} x ] \cap [ \gamma^{2} x, x ] = \{ O \}$ , and let $M$ be the midpoint of $[ x, \gamma x ]$ .

Case 1: $d(M, \gamma x) \leq d(O,\gamma x)$

In this case we have $d(M, \gamma x) = d(M, x) = d(\gamma M, \gamma x)$ . So $\gamma M = M$ , and $\gamma$ is elliptic.

Case 2: $d(M, \gamma x) > d(O, \gamma x)$

Case 2 of Theorem 16

Let $I = [\gamma^{-1} O, O] \subseteq [x, \gamma x]$ . Now $I \cap \gamma I = \{ O \}$ . Therefore $\bigcup\limits_{n \in \mathbb{Z}} \gamma^{n} I$ is isometric to $\mathbb{R}$ and $\gamma$ acts as translation by $[\gamma^{-1}O, O]$ . Furthermore, $d(x, \gamma x) = d(\gamma^{-1}O, O) + 2 d(O, \gamma x)$ . Therefore unless $x$ is on the line just constructed, $d(x, \gamma x) > d(\gamma^{-1} O, O) = |\gamma|$ . $\square$