Author Archive

You are currently browsing opsiser’s articles.

24. Induced graphs of groups and spaces

27 March 2009 in Course notes | Tags: Bass-Serre Theory, Elevations, Graphs of groups | by opsiser | Leave a comment

Our goal is to understand the structure of subgroups of graphs of groups. This will enable us to prove things like: $F \ast_{z} F$ is LERF.

Exercise 22. A group is coherent if every fg subgroup is fp. Prove that $\pi_1$ of a finite graph of groups with coherent vertex groups and cyclic edge group is coherent.

Recall, that if $H \subseteq \pi_1 \mathcal{G}=G$ is fg then H has an induced graph of groups structure. $\mathcal{H} =H \backslash T_H \subseteq H \backslash T$ where T is the Bass-Serre tree of $\mathcal{G}$ .

Topologically, $H$ defines a covering space $X^H \rightarrow X_g$ , which inherits a graph of spaces structure with underlying graph $H\backslash T$ .

$\Gamma' =H \backslash T_H \subseteq H \backslash T$ is a finite connected subgraph and the image of $\Gamma'$ in $X^H$ is a connected subcomplex $X'$ such that $\pi_1 X' = \pi_1 X^H =H$ . $X'$ has the structure of a graph of space with underlying graph $\Gamma'$

There is an explicit algebraic description of $H\backslash T$ , which follows immediately from Lemmas 16,17,18.

Lemma 23. (a) The vertices of $H\backslash T$ are in bijection with $\coprod_{v \in V(\Gamma)} H \backslash G/G_v=\coprod_{v \in V(\Gamma)}\{HgG_v\mid g \in G\}$ .

The vertex $HgG_v$ is labelled by: $H \cap gG_vg^{-1}$ , well-defined up to conjugation in $H$ .

(b) The edges of $H\backslash T$ are in bijection with $\coprod_{e \in E(\Gamma)} H \backslash G/G_e$ . The vertex $HgG_e$ is labelled with $H \cap g G_e g ^{-1}$ .

(c) The edges of $H\backslash T$ adjoining the vertex corresponding to $HgG_v$ are in bijection with $\coprod_{e~\mathrm{adjoining}~v} (g^{-1} H g \cap G_v ) \backslash G_v/G_e$ .

Now we will try to understand this topologically. In particular, we will understand the edge maps of a covering space of a graph of spaces.

Let $f:X \rightarrow Y$ be a continuous map and $Y' \rightarrow Y$ a covering map. If $f':X \rightarrow Y'$ makes the diagram commutes, then $f'$ is a lift of $f$ .

Lemma 24. Fix basepoint $x \in X$ , $y=f(x) \in Y$ , and $y' \in Y'$ mapping to $y$ . There is a lift $f':X \rightarrow Y'$ with $f'(x)=y'$ if and only if $f_{\ast} \pi_1(X,x) \subseteq \pi_1(Y',y')$ . Furthermore, if this lift exists it is unique.

It may be impossible to lift at $y'$ . But it is possible if we pass to a covering space. Eg., if $\tilde{X} \rightarrow X$ is the universal cover. Intuitively, an elevation is a minimal lift.

Definition: Let $X,Y,Y', x,y,y'$ be as above. A based connected covering space $(X',x') \rightarrow (X,x)$ together with a based map $f':(X',x')\to (Y',y')$ such that

elevation1

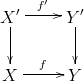
commutes is an elevation (of $f$ at $y'$ ) if whenever the diagram

elevation

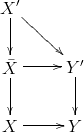
commutes and $X' \rightarrow \bar{X}$ is a covering map of degree larger than 1 then the composition $(\bar{X},\bar{x}) \rightarrow (X,x) \rightarrow (Y,y)$ does not lift to $Y'$ at $y'$ .

The unbased covering map $X' \rightarrow X$ or equivalently the conjugacy class of the subgroup $\pi_1(X') \subseteq \pi_1(X)$ is called the degree of the elevation $f'$ .

7. Cayley Graphs

8 February 2009 in Course notes | Tags: Cayley graphs, Quasi-isometry | by opsiser | Leave a comment

Let $\Gamma$ be a finitely generated group. It has a surjection $F_s \rightarrow \Gamma$ for S finite. Elements of the kernel are called relations and the elements of S are called genereators. Suppose the kernel is generated as a normal subgroup by a subgroup $K \subseteq F_S$ . Then we write $\Gamma \cong \langle S|R \rangle$ to mean $\Gamma \cong F_S/ \langle \langle R \rangle \rangle$ . If R is finite, the $\Gamma$ is said to be finitely presentable.

Example: $\mathbb{Z} \cong \langle b,c|bcb^{-1}c^{-1},b^2c^{-3} \rangle$ .

Let’s develop a topological point of view.

Let $X^{(1)}$ be the standard rose for $F_S$ . Each relation $r \in R$ corresponds to a (homotopy class of a) map $f_r:S^1 \rightarrow X^{(1)}$ . We construct a 2-complex X gluing on a 2-cell using the map $f_r$ for each relation $r \in R$ .

Lemma 6: $\pi_1(X) \cong \Gamma$
Proof: This is a simple application of the Seifert-van Kampen Theorem.

We call X a presentation complex for $\Gamma$ , and we deduce that every finitely generated group is $\pi_1$ of a 2-complex.

Exercise 8: Every finitely presented group is $\pi_1$ of a closed 4-manifold.

Therefore, $\Gamma$ acts freely and properly discontinuously on some 2-complex $\tilde{X}$ , the universal cover of $X$ .

Definition: Let S be a finite generating set for $\Gamma$ as above. Then $Cay_S(\Gamma)=\tilde{X}^{(1)}$ is the Cayley graph of $\Gamma$ with respect to S.

To see that this only depends on S, let’s give the more standard definition. The vertices of $Cay_S(\Gamma)$ are just the elements of $\Gamma$ . For each generator $g \in S$ , two vertices $\gamma ,\delta$ are joined by an edge iff $\gamma g=\delta$

The group $\Gamma$ acts by left translation.

Examples:

$\mathbb{Z}\cong \langle 1\rangle$ .
$\mathbb{Z} \cong \langle 2,3 \rangle$ .
The tree for $F_S$ .

Definition: The Cayley graph $Cay_S(\Gamma)$ induces a natural length metric on $\Gamma$ , denoted $d_S$ and called the word metric. Note that $d_S(1,\gamma)=l_S(\gamma)$ , the word length of $\gamma$ .

The action of $\Gamma$ on $Cay_S(\gamma)$ is by isometries.

Given a metric space $(X,d)$ , a geodesic is just an isometric embedding of a compact interval into $X$ .

A metric space is geodesic if any pair of point is joined by a geodesic. Note that $Cay_S(\Gamma)$ is a geodesic metric space.

Definition: Let $\lambda ,\epsilon \geq 0$ . A $(\lambda,\epsilon)$ -quasi isometric embedding is a map of metric space $f:X \rightarrow Y$ such that $\lambda^{-1}d_X(x_1,x_2)-\epsilon \leq d_Y(f(x_1),f(x_2)) \leq \lambda d_X(x_1,x_2)+\epsilon$ .
If for some $C$ , we also have that for every $y \in Y$ , there is $x \in X$ such that $d_Y(f(x),y) \leq C$ , then $f$ is a quasi-isometry.

Exercise 9: Quasi-isometry is an equivalent relation (use the Axiom of Choice).

Exercise 10: Let $S$ and $S'$ be two finite generating sets for $\Gamma$ . Then $id:(\Gamma,d_S) \rightarrow (\Gamma,d_{S'})$ is a $(\lambda,0)$ quasi-isometry.