Last time:
Lemma 24: Fix basepoints x,y,y' \in X,Y,Y' as usual. There is a lift f':X'\rightarrow Y' of f:X\rightarrow Y such that f(x)=y' if and only if

f_*\pi_1(X,x) \subseteq \pi_1(Y',y').

Furthermore, if the lift exists, it is unique.

Lemma 25: Given a choice of y', there exists an elevation f':X'\rightarrow Y' of f:X\rightarrow Y at y'. Furthermore, f' is unique in the sense that if \bar{f}:\bar{X}\rightarrow Y' is another elevation of f and y' then there is a homeomorphism X'\rightarrow \bar{X} and the diagram

Image 1

commutes.

Proof:

Image 2

Let (X',x')\rightarrow (X,x) be defined by \pi_1(X',x')=f^{-1}_*\pi_1(Y',y'). By Lemma 24, the composition

(X',x')\rightarrow (\bar{X},\bar{x})\rightarrow (Y,y)

lifts at y', call this lift f'. Suppose

Image 3

Then \pi_1(X',x')\subseteq \pi_1(\bar{X}\bar{x}). But by Lemma 24, f_*\pi_1(\bar{X},\bar{x})\subseteq \pi_1(Y',y'). This implies \pi_1(X',x') =\pi_1(\bar{X},\bar{x}).

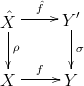
Another, more categorical construction uses the fibre product.

Image 4

The fibre product \hat{X} is defined by

\hat{X} =\{(\xi,\eta)\in X\times Y'|f(\xi)=\sigma(\eta) \}.

There are obvious maps

\hat{X}\stackrel{\hat{f}}{\rightarrow} Y'
\hat{X}\stackrel{f}{\rightarrow} X

given by forgetting factors.

Exercise: If \sigma is a covering map then \rho is a covering map.

Lemma 26: Fix x\in X. Let y=f(x)\in Y and let \sigma(y')=y for y'\in Y. Let x'=(x,y')\in \hat{X}, and let X\subseteq\hat{X} be the connected component containing x'. Then f'=\hat{f}|_{x'}:X'\rightarrow Y' is an elevation of f at y', and every elevation of f arises in this way.

Proof: To prove that f' is an elevation we just observe that p_*\pi_1(X',x')=f_*^{-1}\sigma_*\pi_1(Y,'y'). Now suppose

Image 5

is an elevation. Then \bar{X}\rightarrow \hat{X}=\{(\xi,\eta)|f(\xi)=\sigma(\eta) \}, with \xi\mapsto(\tau(\xi),\bar{f}(\xi)).

The covering map \tau factors trhough \bar{X}\rightarrow\hat{X}, and so \bar{X}\mapsto\hat{X} is a covering map. Because \bar{X} is an elevation, \bar{X}\mapsto\hat{X} is a homeomorphism onto its image, a connected component of \hat{X}.

What has this got to do with graphs of spaces/groups?

Let Y be a vector space, and let \partial: E\rightarrow Y be an edge map. Define X to be the mapping cylinder

X =(E\times[0,1]) \sqcup Y/\sim ;\;\; (x,1)\sim\partial(x)

X comes with a map d:X\rightarrow Y such that d|_Y=id_Y and d(x,t)=\partial(x). This is an inclusion \iota:Y\rightarrow X, and d\circ\iota =id_Y. Let \sigma:Y'\rightarrow Y be a covering map.

Image 6

Let \hat{X} be the fibre product. There’s a map \iota':Y'\rightarrow \hat{X}; \eta\mapsto (\iota\circ\sigma (\eta),\eta). Clearly, d'\circ\iota'=id_{Y'}.

Therefore, \iota' is an injection. It’s easy to see that \iota' induces a bijection at the level \pi_0.

Lemma 27: Any covering space X'\rightarrow X arises as the fibre product of a covering map Y'\rightarrow Y.

Proof: Let \tau:X'\rightarrow X be a covering map

Image 7

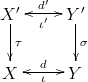
let Y' be the fibre product of \tau and \iota.

Y'=\{(\xi,\eta)\in X'\times Y |\tau(\xi)=\iota(\eta)\}

Define d':X'\rightarrow Y' by \xi\mapsto (\xi,d\circ\tau(\xi)). As before, \sigma is a covering map.