You are currently browsing the tag archive for the ‘Free groups’ tag.
Theorem 12 (Gromov): Let be torsion-free
-hyperbolic group. If
such that
, then for all sufficiently large
,
.
Remark: The torsion-free hypothesis is not necessary, but it allows us to avoid some technicalities. For instance, it is a non-obvious fact that an infinite hyperbolic group contains a copy of .
For the rest of this lecture will be a torsion-free
-hyperbolic group,
where
are primitive (i.e. not proper powers).
Recall that for torsion-free
-hyperbolic,
primitive implies that
.
If and
do not commute we can show there is some point
on
arbitrarily far from
.
 Hence we have the following lemma.
Hence we have the following lemma.
Lemma 13:
If and
do not commute there is some point
on
arbitrarily far from
.
Proof: Suppose not. That means such that
such that
. So
is in
. But the Cayley graph is locally finite so
has finitely many elements. By the Pigeonhole Principle
such that
for some
. Then
. But then
.
.
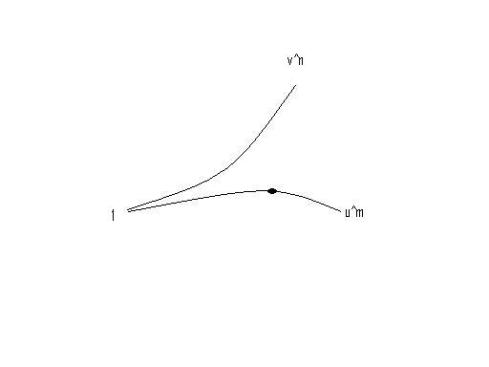
For a moment view and
as the horizontal and vertical geodesics in
. For two points
on
and
on
, we can argue that the geodesic between them curves toward the origin.
 And so we have Lemma 14.
And so we have Lemma 14.
Lemma 14: There exists such that
,
.
Proof:
 Recall that
Recall that by
is a quasi-isometric embedding. So by Theorem 6,
and
 By Lemma 13 choose
By Lemma 13 choose such that
. Choose
such that
. Now,
must be
-close to
so for some point
on the geodesic between
and
,
. Then
.
For a subgroup , one can choose a closest point projection
which is
-equivariant. (Write
. Choose
where
and
are close and declare
to be
-equivariant.)
is typically not a group homomorphism.
We’re interested in and
.
 In
In , there is some
such that
either
or
.

Lemma 15: such that
,
or
.
Proof:
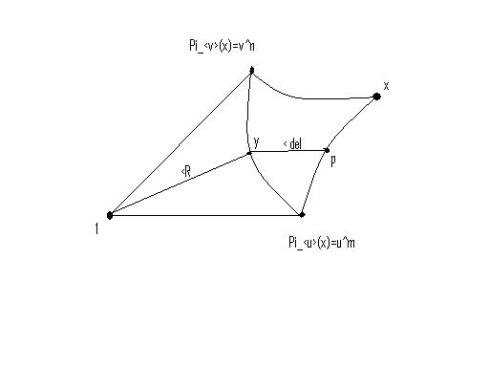
Let . WLOG,
is
-close to
and
since
is the closest point to
(in particular compared to
). So
.
.
Now we can prove the theorem.
Proof of Theorem 12:
The idea is to use the Ping-Pong Lemma on the Cayley graph.
 Let
Let and let
, where
is provided by Lemma 15. For all
we have
and likewise for all
we have
. In particular,
.
Let . By
-equivariance,
for any . In particular,
by the triangle inequality. Similarly,
for all and all
. Because
and
are quasi-isometrically embedded, it follows that
and
for
.
Therefore, by the Ping-Pong Lemma .
Fact: There exists a finitely generated non-Hopf group. (An example is the Baumslag-Solitar group , although we cannot prove it yet.) So, by Lemma 5, there is a finitely generated non-residually finite group. Thus, free groups are not ERF: if
is a finitely generated non-residually finite group, then Lemma 4 implies that the kernel of a surjection
is not separable in
. However, finitely generated subgroups of free groups are separable:
Marshall Hall’s Theorem (1949): is LERF.
This proof is associated with Stallings.
Proof: As usual, let where
is a rose. Let
be a covering map with
finitely generated. Let
be compact. We need to embed
in an intermediate finite-sheeted covering.
Enlarging if necessary, we may assume that
is connected and that
. Note that we have
. By Theorem 5 (see below), the immersion
extends to a covering
. Then
. So
lifts to a map
.
The main tool in the proof above is this:
Theorem 5: The immersion can be completed to a finite-sheeted covering
into which
embeds:

Proof: Color and orient the edges of . Any combinatorial map of graphs
corresponds uniquely to a coloring and orientation on the edges of
. A combinatorial map is an immersion if and only if at every vertex of
, we see each color arriving at most once and leaving at most once. Likewise, it’s a covering map if and only if at each vertex, we see each color arriving exactly once and leaving exactly once.

Let be the number of vertices of
. For each color
, let
be the number of edges of
colored
. Then there are
vertices of
missing “arriving” edges colored
, and there are
vertices of
missing “leaving” edges colored
. Choose any bijection between these two sets and use this to glue in
edges colored
. When this is done for all colors, the resulting map
is clearly a covering.
Note that the proof in fact gives us more. For instance:
Exercise 6: If is a finitely generated subgroup of
, then
is a free factor of a finite-index subgroup of
.
Exercise 7 (Greenberg’s Theorem): If and
is finitely generated, then
is of finite index in
.
Ping-Pong Lemma
Question. Let G be a group and . When is
?
Ping-Pong Lemma: Let G be a group acting on a set X and . Assume:
- a and b have infinite orders.
- There exist
such that
and
,
for all
.
Then .
Proof. Consider such that
and
. Choose a reduced word w for a nontrivial element in
, i.e., either
or
and
.
Case 1: . Then
and
, so
and
, and so on until
, so
. Therefore
.
Case 2: . Then, by Case 1,
, so
. Therefore
.
Case 3: . (similar to above)
Case 4: . (similar to above)
Free Groups Are Linear
Theorem 3. is linear.
Proof. acts on
by linear transformations. Let
and
. Then
and
. Let
and
. Then
for all
, so
by the Ping-Pong Lemma.
Corollary 1. Finitely generated free groups are linear, hence residually finite.
Proof. The case of is obvious; otherwise, this follows from
as proved in Exercise 1.
Separability
Definition. Let G be a group. The profinite topology on G is the coarsest topology such that every homomorphism from G to a finite group (equipped with the discrete topology) is continuous.
Definition. A subgroup H is separable in G if H is closed in the profinite topology of G.
Exercise 3. Let G be a group. is separable if and only if for all
, there exists a homomorphism to a finite group
such that
. Note that if X = {1}, this is equivalent to: G is RF if and only if {1} is separable.
Hint. For the “if” direction, let and consider
. For the other direction, use the definition of subbase and that
.
Definition. Let G be a group.
- G is Extended RF (ERF) if any subgroup of G is separable.
- G is Locally ERF (LERF, subgroup separable) if any finitely generated subgroup is separable.
Lemma 3. Let G be a group. A subgroup H of G is separable if and only if for all , there exists a finite-index subgroup
such that
and
.
Proof. In the “only if” direction, by the previous exercise, for all , there exists a homomorphism to a finite group
such that
. Then
. Conversely, let
. By hypothesis, there exists a finite-index subgroup
such that
and
. Let
. Note that this is a finite number of intersections (
, to be precise). There exists a finite quotient
. Then
. Therefore,
, i.e.,
, and the lemma follows by the previous exercise.
Scott’s Criterion (1978). Let X be a Hausdorff topological space and . Let
be a covering and
. Then H is separable in G if and only if for any compact
, there exists and intermediate finite-sheeted cover
such that
embeds
into
.
Exercise 4. Let be a separable subgroup.
- If
, then
is separable in G’.
- If
has finite index, then
is separable in G’.
Recent Comments